구문론과 의미론
1. 언어의 형식적 정의
- 구문론과 의미론을 통해 언어를 엄밀하게 정의.
- 구문론 (syntax) : 문장이 구성되는 방식에 대해 연구
- 의미론 (semantics) : 문장이 나타내는 의미에 대해 연구
- ex) 나는 너를 사랑한다.
ㄴ 구문 : 주어 + 목적어 + 서술어
ㄴ 의미 : 화자가 청자를 몹시 아끼고 귀중히 여긴다.
- ex) I love you
ㄴ 구문 : 주어 + 서술어 + 목적어
ㄴ 의미 : 상동
ㄴ 의미는 같지만 언어가 다르기 때문에 구문(형식)이 다름!
2. 프로그래밍 언어의 형식적 정의
- 프로그래밍 언어의 명확한 구문과 의미를 정의
- 이를 통해 명확한 사용체계를 제공
- ex) print "GCD is"; A (<--- BASIC 언어)
ㄴ 구문 : PRINT "출력할 내용"; 변수
ㄴ 의미 : 출력할 내용과 변수의 값을 순차적으로 출력하라.
- ex) printf("GCD is %d, a);
ㄴ 구문 : printf("출력할 내용", 변수); (<--- C, C++ 언어)
ㄴ 의미 : 출력할 내용의 %d 자리에 변수의 값을 대신 넣어 내용을 출력하라.
ㄴ 결과값은 똑같고 의미도 비슷하지만, 다른 언어라서 구문은 다름.
- 형식적 정의의 필요성
ㄴ 컴퓨터 : 프로그램 해석의 모호함 제거
ㄴ 작성자 : 프로그램의 동작 예측 가능
- ex) 예시를 위한 가상의 언어
int x12;
x12 = 1 + 5 * 2;
if x12>10 then ...(1) 프로그램의 구조
ㄴ 문자 : 영어 알파벳, 아라비아 숫자, 특수기호 등
ㄴ 어휘(토큰) : 문자의 모임, 최소한의 의미를 갖는 단어
ㄴ 구문 : 프로그램을 작성하는 규칙.
ㄴ 토큰을 모아 프로그램을 구성.
(2) 프로그램의 의미
ㄴ 의미 : 프로그램을 통해 발생하는 현상
ㄴ 정수를 저장할 변수 x12를 만든 다음
수식을 계산하여 11을 변수 x12에 대입하고
변수 x12의 값이 10보다 크므로 ... 부분을 수행.
2-1. 프로그래밍 언어의 형식적 정의
1) 구문론
- 프로그램의 표면적인 구조를 정의
- 프로그램 작성 시, 어떤 형태로 작성해야 하는지를 기술
2) 의미론
- 프로그램의 내용적인 효과를 정의
- 프로그램 실행 시 어떤 일이 일어나는지 그 의미를 기술
구문의 표현
1. 구문론
- 프로그램의 표면적인 구조를 정의
- 정의된 구문을 통해 모든 정상적인 프로그램을 도출
- 작성된 프로그램이 정의된 구문에 맞는 프로그램인지 확인
- 구문의 표현 :
ㄴ 구문의 정의는 문법을 활용하여 명확하게 표현
ㄴ 일반적으로 프로그래밍 언어에서는 문맥 자유 문법을 이용
2. 문맥 자유 문법(CFG : Context-Free Grammar) <-- 컴파일러 과목에서 더 자세히 배울 예정.
1) 구성요소 4가지
(1) 비단말 기호 : 정의될 대상.
ㄴ ex) '대입문' 비단말 기호.
(2) 단말 기호 : 언어에서 직접 사용되는 표현.
ㄴ 프로그램을 작성했을 때, 그 프로그램에 직접 드러나는 단어들. 직접 눈에 보이는 것들.
ㄴ ex) int, 변수이름 x12, 숫자 0, 숫자 1, 더하기 기호 + , 등등...
(3) 시작 비단말 기호 : 언어에서 독립적으로 사용될 수 있는 단위.
ㄴ 비단말 기호 중, 시작 지점으로 사용할 수 있는 애들.
(4) 규칙 : 하나의 비단말 기호를, 단말 기호와 비단말 기호의 조합으로 정의.
ㄴ 하나의 규칙은 하나의 비단말 기호만을 정의해야 한다.
ㄴ ex) 대입문 정의 시, '대입문은 무엇이다.' 이렇게 하나만 정의해야함.
대입문과 조건문, 두 가지 비단말 기호를 한꺼번에 묶어서 정의하면 안 된다.
(5) 예시
| <if문> ::= if <논리식> then <문장> |
ㄴ <if문>, <논리식>, <문장> : 비단말 기호
ㄴ if, then : 단말 기호
3. 문맥 자유 문법의 다양한 표현 방법
1) BNF
2) EBNF
3) 구문 도표
구문론 > 문맥 자유 문법 > 표현 방법
1. BNF (24min)
- BNF : Backus-Naur Form. 이 두 사람이 만든 form.
- Algol의 구문을 정의하기 위해 사용된 표기법.
- 메타 기호 세 가지
: (1) ::= (정의) (2) | (택일) (3) <> (비단말 기호)
- 비단말 기호 : <>로 묶인 기호
- 단말 기호 : 비단말 기호 및 메타 기호가 아닌 기호.
ㄴ 정의, 택일, 비단말 기호가 아닌 것. 즉, 둘이 아닌 '나머지' 같은 존재.
- 규칙 : ::=를 기준으로 왼쪽 부분을 오른쪽 부분으로 정의.
| <if문> ::= if<논리식> then <문장> else <문장> | if <논리식> then <문장> |
ㄴ 비단말 기호 : <if문>, <논리식>, <문장>, <문장>, <논리식>, <문장>
ㄴ 이 중 시작 비단말 기호 : <if문>
ㄴ 메타기호 :
ㄴ (1) ::== 정의
(2) | 택일
(3) 비단말 기호
ㄴ 단말기호 : if, then, else, if, then
ㄴ 해석 : if문은, | 왼쪽 것이거나, | 오른쪽 것이다.
즉, if문은 (1) if<논리식> then <문장> else<문장> 이거나 (<-- else 있는 if문)
(2) if<논리식> then<문장> (<-- else 없는 if문)
으로 정의된다.
2. EBNF (31min)
- EBNF : Extended BNF. 즉, BNF를 확장시킨 것.
- BNF에 추가적인 메타 기호를 사용하여 규칙을 보다 간결하게 표현
- 추가된 메타 기호 :
(1) [ ] : 생략 가능
(2) { } : 0번 이상 반복한다
(3) ( ) : |과 함께 쓰여 한정된 범위의 택일
(4) ' ' : 메타 기호를 단말 기호로 사용
ㄴ ' ' 안에 메타기호가 들어 있다면, 그 메타 기호 자체를 단말 기호로 바꿔서 사용해준다.
ㄴ ' ' 안에 들어간 메타기호는, 더 이상 어떤 의미가 있는 메타 기호가 아니라, 단말기호로 나는 사용하겠다 라는 뜻.
- ex1) [ ] 예시
※ [ ] : 생략 가능
| EBNF <if문> ::= if <논리식> then <문장> [ else <문장> ] |
ㄴ 이걸 BNF로 표현하면 아래와 같다.
| BNF <if문> ::= if<논리식> then <문장> else <문장> | if <논리식> then <문장> |
ㄴ EBNF가 BNF보다 훨씬 간결하게 정의된 것을 확인할 수 있다.
ㄴ EBNF --> BNF :
EBNF에서 [ ] 이었던 애를
[ ] 있는 경우
| [ ] 없는 경우
으로 나타냈음을 알 수 있다.
- ex2) { } 예시
※ { } : 0번 이상 반복한다
| EBNF <unsigned integer> ::= <digit> { <digit> } |
ㄴ 부호가 없는 정수는,
ㄴ { } 가 0번 이상 반복이니까, 0번 반복되면 한자리 정수를, 1번 반복되면 두자리 정수를, 2번 반복되면 세자리 정수를, ....
이렇게 해서 모든 정수를 정의할 수 있게 됨.
ㄴ 이걸 BNF로 표현하면 아래와 같다.
| BNF <unsigned integer> :: = <digit> | <unsigned integer> <digit> |
ㄴ 재귀적으로 정의했다. ex1) 과 마찬가지로 EBNF가 BNF보다 훨씬 간결하게 표현할 수 있음을 보여준다.
ㄴ EBNF --> BNF :
EBNF에서 { } 이었던 애를
{ } 없는 경우
| { } 있는 경우 (재귀적)
으로 나타냈음을 알 수 있다.
- ex3) ( ) 예시
※ ( ) : |과 함께 쓰여 한정된 범위의 택일
| EBNF <수식> ::= <수식> ( + | - | * | / ) <수식> |
ㄴ <수식>과 <수식> 사이에 + 또는 - 또는 * 또는 / 가 있다.
| BNF <수식> ::= <수식> + <수식> | <수식> - <수식> | <수식> * <수식> | <수식> / <수식> |
ㄴ EBNF --> BNF :
( ) 바깥의 부분을 반복하여 표현
ㄴ BNF에서의 택일 기호 : 자신의 왼쪽에 있는 것을 선택하거나 오른쪽에 있는 것을 선택한다.
EBNF와 달리 BNF에서는 ( ) 을 사용한 범위 제한이 없기 떄문에, ::= 정의기호 이후의 모든 것들에 해당한다.
따라서,
step1. <수식> ::= <수식> + <수식>
| <수식> - <수식> | <수식> * <수식> | <수식> / <수식>
step2. <수식> ::= <수식> + <수식>
| <수식> - <수식>
| <수식> * <수식> | <수식> / <수식>
step3. <수식> ::= <수식> + <수식>
| <수식> - <수식>
| <수식> * <수식>
| <수식> / <수식>
- ex4) ' ' 예시
※ ' ' : 메타 기호를 단말 기호로 사용
| EBNF <BNF 규칙> ::= <왼쪽 부분> '::=' <오른쪽 부분> |
[참고] BNF를 EBNF로 변환하는 방법 은 링크 참조.
3. 구문도표 (40min)
- 초기 Pascal의 사용자 설명서에 사용된 표현법
- 순서도와 유사하게 그림으로 구문을 표현
(1) 사각형 : 비단말 기호
(2) 원 : 단말 기호
(3) 화살표 : 비단말 기호 및 단말 기호들을 연결. 규칙.
- ex1)
| EBNF <if문> ::= if <논리식> then <문장> [ else <문장> ] |

- ex2)
| EBNF <수식> ::= <수식> ( + | - | * | / ) <수식> |

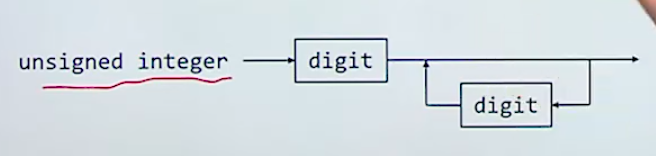
- ex3)
| ENBF <unsigned integer> ::= <digit> { <digit> } |
의미의 표현
1. 의미론 (49min)
- 프로그램의 내용적인 효과를 정의
- 프로그램 실행 시 어떤 일이 일어나는지 그 의미를 기술
- 구문으로 표현하기 어려운 제약사항을 기술하기도 함
- 의미의 표현 :
ㄴ 일반적으로 자연어 문장으로 표현하나 명확성이 부족
ㄴ 의미의 엄밀한 표현을 위한 다양한 기법 개발 (형식 의미론)
2. 형식 의미론 (51min)
1) 정적 의미론
- 정적 : 프로그램이 수행되기 이전의 상태.
- 프로그램을 수행하기 전 의미가 맞는지 파악하는 방법
- 주로 타입 검사 수행에 활용
- 대표적인 방법 : 속성 문법
2) 동적 의미론
- 동적 : 프로그램이 수행되고 있는 상태.
- 프로그램 수행 시 나타나게 될 의미를 표현하는 방법
- 대표적인 방법 : 기능적 의미론, 표기적 의미론, 공리적 의미론 등
3. 정적 의미론 방법 예시
1) 속성 문법 (53min)
- 비단말 기호마다 타입 속성이 있다고 가정하고 이에 대한 규칙을 정의
- ex)
| BNF <D> : : = <T> <id> <L> ; // D : Declaration. 선언하는 부분. / T : 타입 이름. // id : 변수 이름. / L : 변수 이름들의 리스트. (여러 변수를 한꺼번에 선언하고 싶을 때) // 즉, 변수를 선언하려면, 타입 이름 + 변수 이름 + 변수 이름 리스트 + ';' 하면 된다. <T> : : = int | char // T (타입이름)은 int 또는 char 이다. <L> : : = <id> <L> | ε // 변수 이름 리스트는, |
속성 문법)
| 구문 규칙 | >> 타입 속성 규칙 << |
| <D> : : = <T> <id> <L> ; <T> : : = int | char <L> : : = <id> <L1> | ε |
id . t = T . t ∧ L . t = T . t T . t = 정수 T. t = 문자 id . t = L . t ∧ L1 . t = L . t |
※ ε : empty. '아무것도 없다'는 뜻.
4. 동적 의미로 방법 예시
1) 기능적 의미론
- 추상기계의 상태를 바꾸는 것으로 수행 의미를 표현
ㄴ 프로그램이 수행(기능)되면 컴퓨터의 상태가 바뀜
ㄴ 상세설명) 프로그램이 동작하면 메모리상에 있는 변수의 값이 바뀌거나 읽어 오거나
그 변수의 상태, 메모리의 상태 값이 계속 바뀐다. 즉, 컴퓨터의 상태가 바뀌는 것.
즉, 메모리의 상태를 주요한 수행 상태, 수행의 의미라고 본 것.
- 상태 : <수행할 명령어, 메모리 상태>
- ex)
| < z=x; x=y; y=z; , [ x→5, y→7, z→0 ] > ⇒ < x=y; y=z; , [ x→5, y→7, z→5 ] > ⇒ < y=z; , [ x→7, y→7, z→5 ] > ⇒ < , [ x→7, y→5, z→5 ] > |
ㄴ line1) z에 x값 대입, x에 y값 대입, y에 z값 대입하라는 뜻. 현재 메모리 상태는 x의 값은 5, y/z는 각각 7,0.
ㄴ line2) z에 x값을 대입하라는 명령을 수행한 결과.
ㄴ line3) x에 y값을 대입하라는 명령을 수행한 결과.
ㄴ line4) y에 z값을 대입하라는 명령을 수행한 결과. 최종 결과.
===> 즉, 세 가지 명령어들이 수행되면서 그때그때 상태가 변화된 것을 변수 값의 변화로 표현했음.
즉, 기능적 의미론에서는 프로그램이 수행되면서 변수값들이 어떻게 변화되는지를 구체적으로 나타내고 있다.
2) 표기적 의미론
- 구문 요소를 수학적 표기에 대응시켜 수행 의미를 표현
- 의미함수 : 대응시키는 함수
- ex)
| <B> : : = 0 | 1 | <B> 0 | <B> 1 |
ㄴ B : 이진수.
ㄴ 즉, 이진수는 010101... 이런식으로... 0과 1로 구성되었다는 것을 재귀적으로 표현했음.
| 구문 규칙 | >> 의미함수 Bin << |
| <B> : : = 0 | 1 | <B> 0 | <B> 1 |
Bin[[ 0 ]] = 0 Bin[[ 1 ]] = 1 Bin[[ B 0 ]] = 2 * Bin[[ B ]] Bin[[ B 1 ]] = 2 * Bin[[ B ]] + 1 |
ㄴ 우측 표기적 의미론 방법 설명)
ㄴ Bin (바이너리)라고 하는 의미 함수를 정의함
ㄴ 함수에 인자로 들어가는 부분은 규문 규칙에서 사용된 것들임.
ㄴ Bin[[ 0]] (한자리 이진수 0) , Bin[[ 1 ]] (한자리 이진수 1) ,
Bin[[ B 0 ]] (0으로 끝나는 여러자리 이진수), Bin[[ B 1]] (1로 끝나는 여러자리 이진수)
이 네 가지의 경우에, 왼쪽의 구문에 사용된 네 가지를 인자로 받아서,
각각의 경우에 바이너리 의미 함수는 어떤 계산을 해줘야 하는지를 오른쪽 실제 수식으로 계산한다.
3) 공리적 의미론 (1hr 06min)
- 프로그램의 효과로 수행의 의미를 표현.
- 효과 : 프로그램 S가 실행됨으로써 사전조건 P를 사후조건 Q로 변화시킴. {P} S {Q}
- 대입문의 효과 공리 : {Q[x→E]} x = E; {Q]
- ex)
| {P} a = b * 2; { a < 10 } - P ⇔ (a < 10}[a→b*2] ⇔ b * 2 < 10 ⇔ b < 5 - {b < 5} a = b * 2; {a < 10} |
ㄴ line1) a라는 변수에 b*2한 값을 대입하겠다. 그리고 이것의 사후 조건은 a<10 이다.
ㄴ line2) 1hr 07min....
5. 의미론의 한계 및 효과
1) 한계
- 프로그래밍 언어 전체에 대한 의미 표현은 너무 복잡하다.
2)효과
- 프로그램의 구현 및 분석 등에 유용하게 사용됨
- 속성 문법 : 인터프리터 및 컴파일러 구현 시 트리 생성, 타입 검사, 코드 생성 등을 할 때.
- 수학적 표기 : 언어의 특성을 명확하게 정의해야 할 때
- 공리적 의미론 : 프로그램의 특정 조건 만족 여부를 확인할 때
참고링크
https://hcr3066.tistory.com/122
이 글이 도움이 되었다면
↓ 왼쪽 아래 ♡ 버튼을 클릭해주세요! :)
'Programming > Computer Science' 카테고리의 다른 글
| [빅데이터의 이해] 4. 빅데이터의 활용2 (0) | 2021.09.10 |
|---|---|
| [빅데이터의 이해] 3. 빅데이터의 활용1 (0) | 2021.09.09 |
| [빅데이터의 이해] 2. 빅데이터의 정의2 (0) | 2021.09.09 |
| [빅데이터의 이해] 1. 빅데이터의 정의 1 (0) | 2021.09.09 |
| [프로그래밍 언어론] 3. 프로그래밍 언어 패러다임 (0) | 2021.09.09 |
| [프로그래밍 언어론] 2. 프로그램 언어의 발전 및 동작원리 (0) | 2021.09.07 |
| [프로그래밍 언어론] 1. 프로그래밍 언어 소개 (1) | 2021.09.07 |
| [운영체제] 운영체제의 구성, 프로세스, 쓰레드 (0) | 2021.04.08 |